MODELLING
Tipping points, nonlinear feedbacks, hidden parameters, retarted loops, synchronization - in many complex systems nonlinear phenomena determine the dynamics.
GOLDBERG ANALYTICS helps to discover such characteristics by AI algorithms, analysis and coarse-grained modelling. But, meaningful models require more than mathematical expertise. That is why we flank our scientific expertise with human intuition and life experience. Participate and tell us about your challenges.
See examples of GOLDBERG ANALYTICS modelling applications:

Body Language and Movement
Thinking of body languages and their relation between music and dance is a field of tension which is very complex. This mind map might gives a first impression. Music, Effort, Perception, Rhythm, Movement, Balance,Cognition, Awareness, Expression, Emotion, ... , there is no doubt that one enters a multi-modal context.
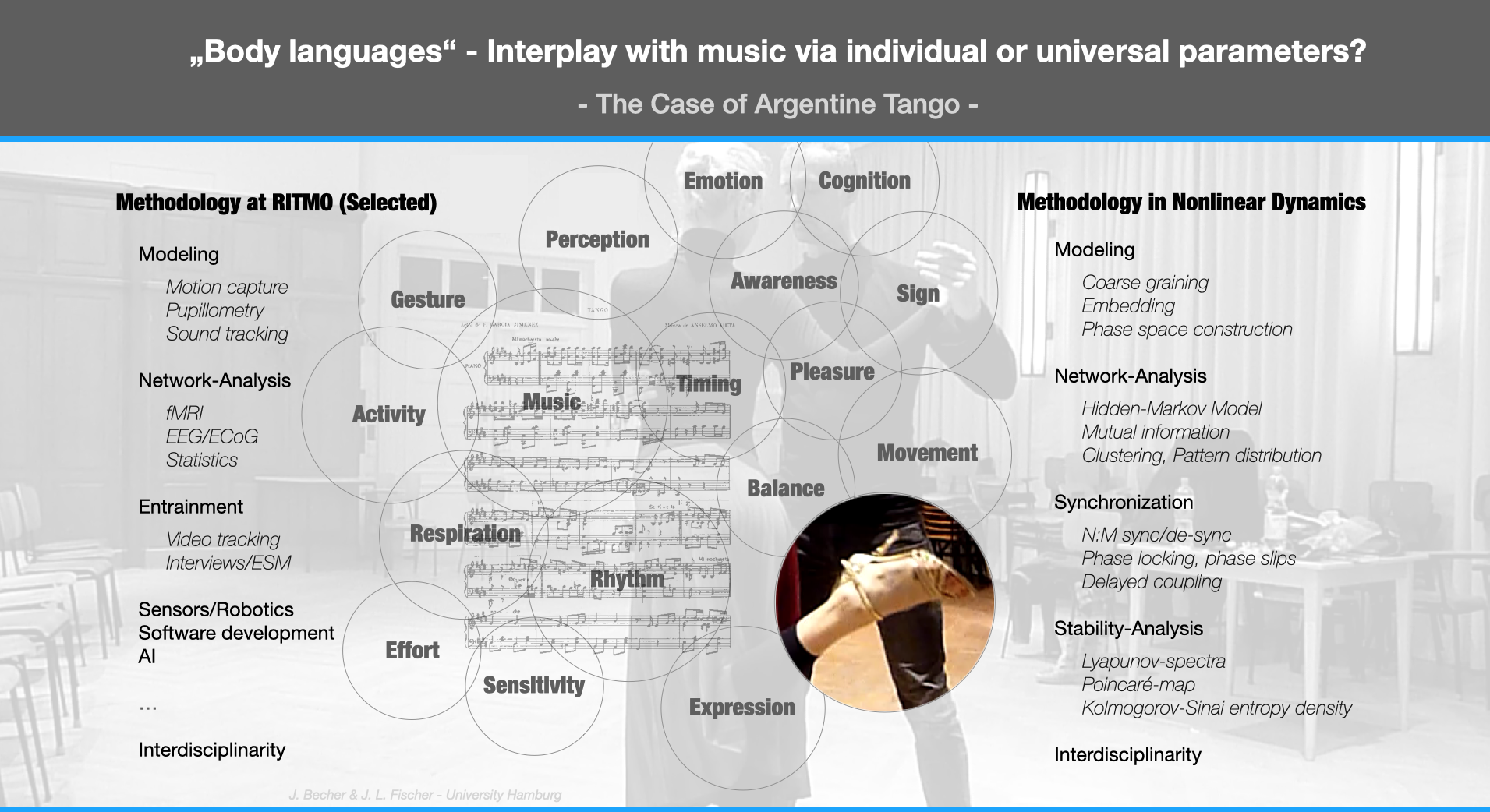
With coarse graining it is possible to transform complex systems into phase space representations. This allows to study the dynamics detached from properties that do not contribute.
Network and Stability-Analysis help to find adequate model structures. With Hidden-Markov-models we are able to identify minimal training efforts and optimal learning pathes. In addition, interviews are a powerful instrument to control the modeling process.
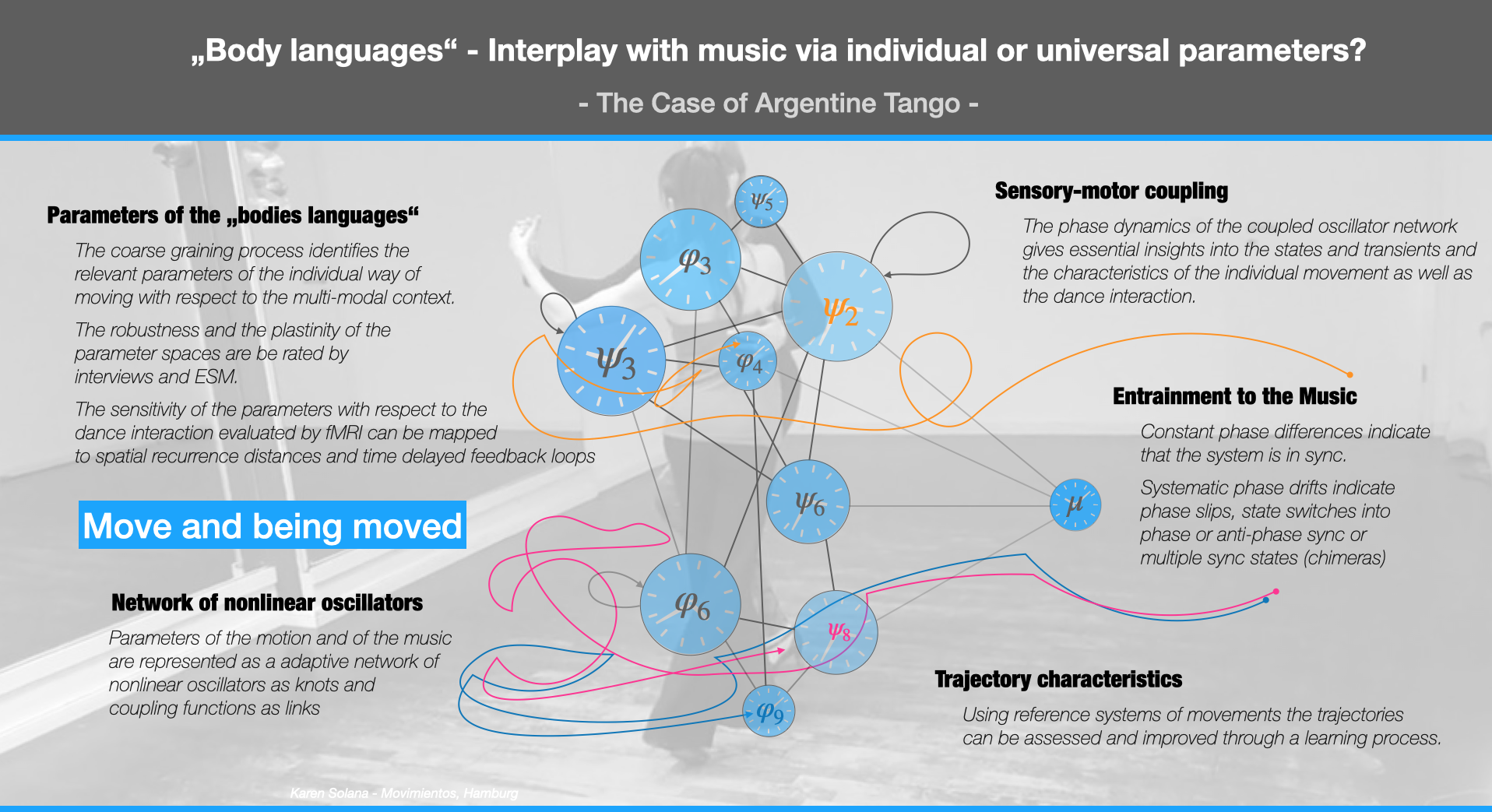
Phenomenona of entrainment are well-studied in nonlinear dynamics. This interesting phenomenon, which is called synchronization in physics, can only occur in nonlinear systems! It is characterized by phase locking and phase transitions.
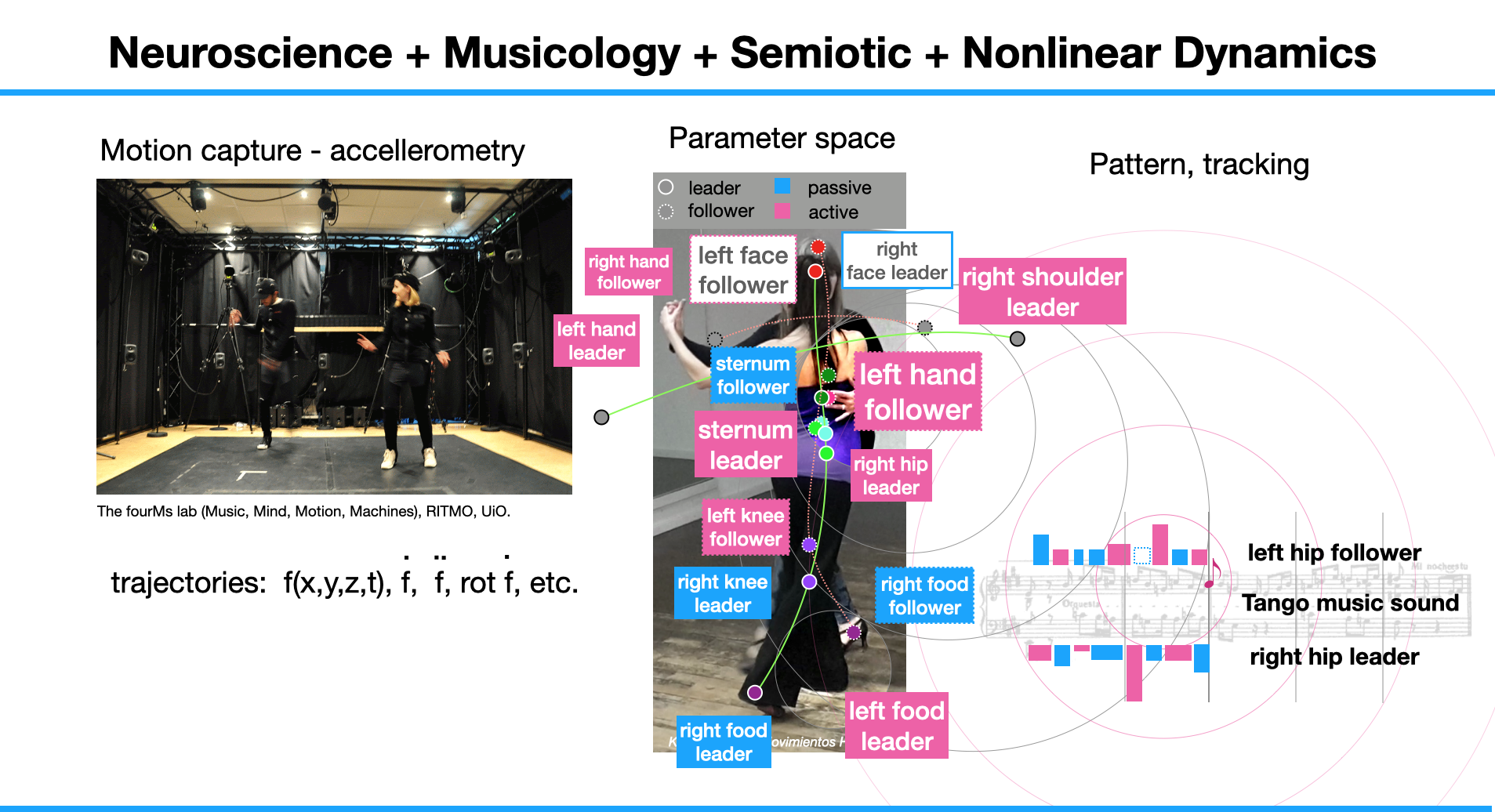
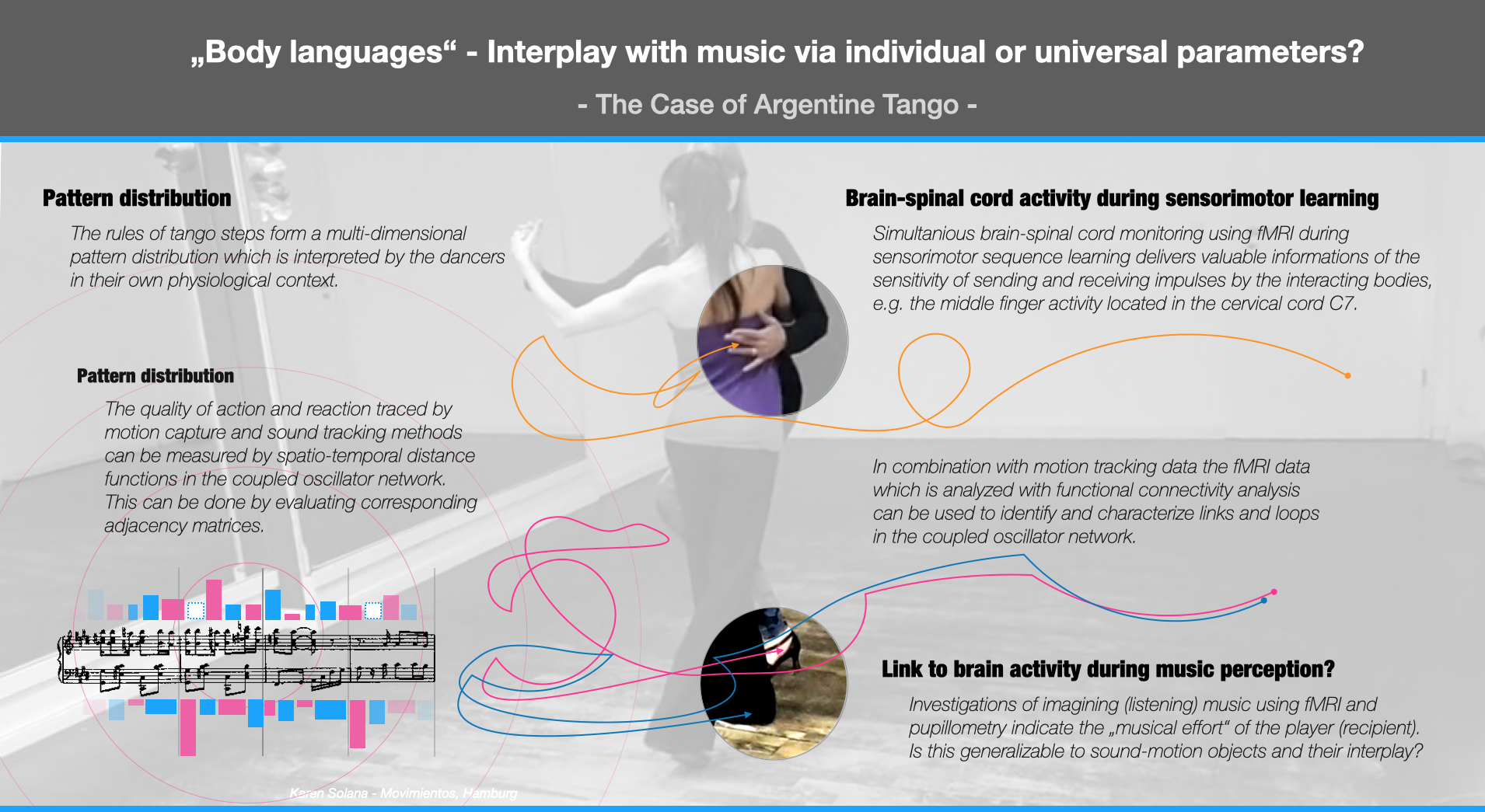
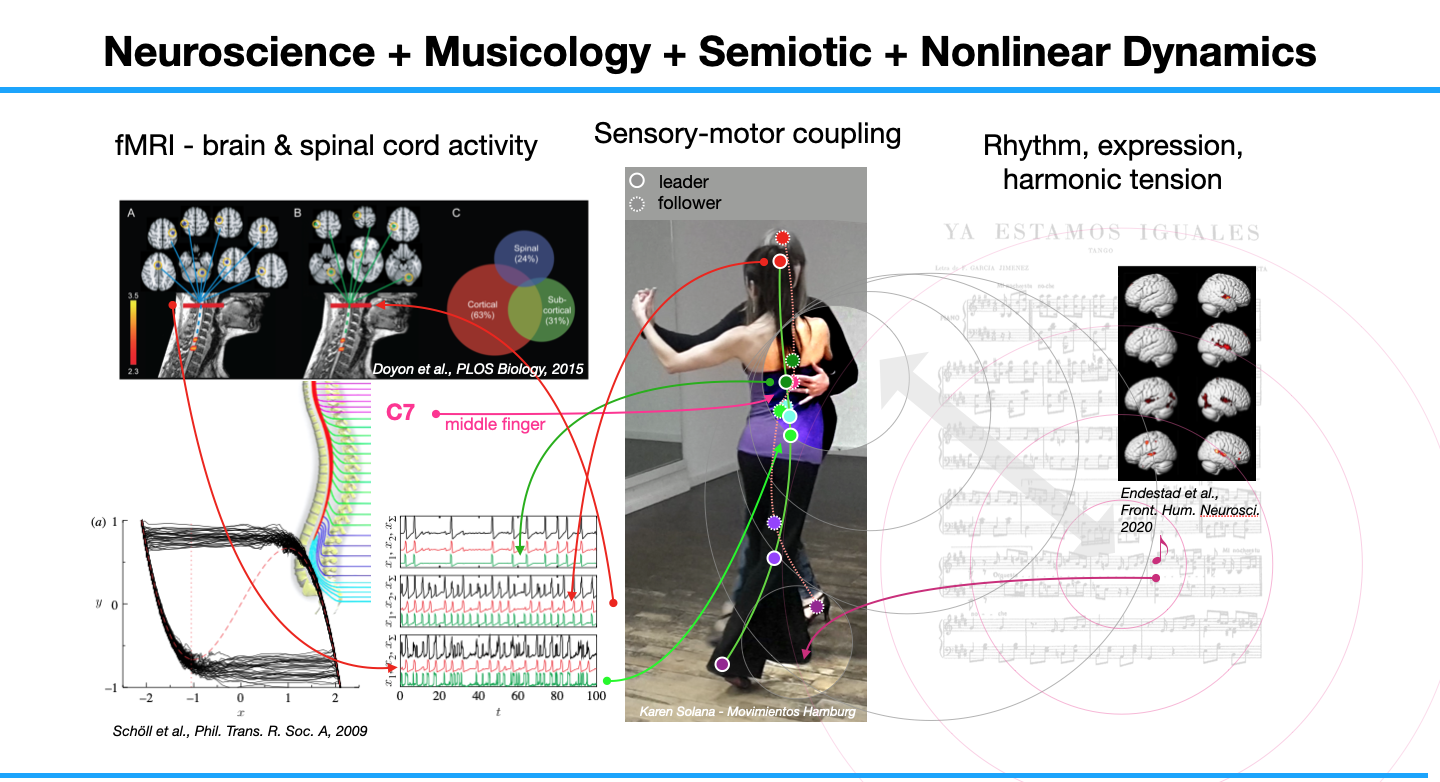
To dicover the sensori-motor learning we utilize fMRI data of brain (LC) and spinal cord activity (C7), motion capture data of dance movement manifolds and sound tracking. This is being accompanied by interviewing and experience sampling (ESM). The transformation into a corresponding coupled phase model helps to find hidden parameters which control the interaction - or - in the best case: which lead to synchronization - one of the secret pleasures of moving and being moved.
Acoustic Synchronization
Synchronization is a highly nonlinear phenomenon in nature. Examples are the synchronized behavior of an auditorium applauding, neuronal networks or populations that synchronize their dynamics in ecosystems. Synchronization can occur when special oscillating systems - so called self-sustained oscillators - interact to each other or with simpler vibrating systems, so called drivers.
GOLDBERG ANALYTICS helps organ builders to design their instruments under given constraints of construction in concert halls and churches. Experiments show the conditions under which synchronization occurs


From the experimental data we extract synchronization plateaus in accordance the theory of nonlinear oscillations.
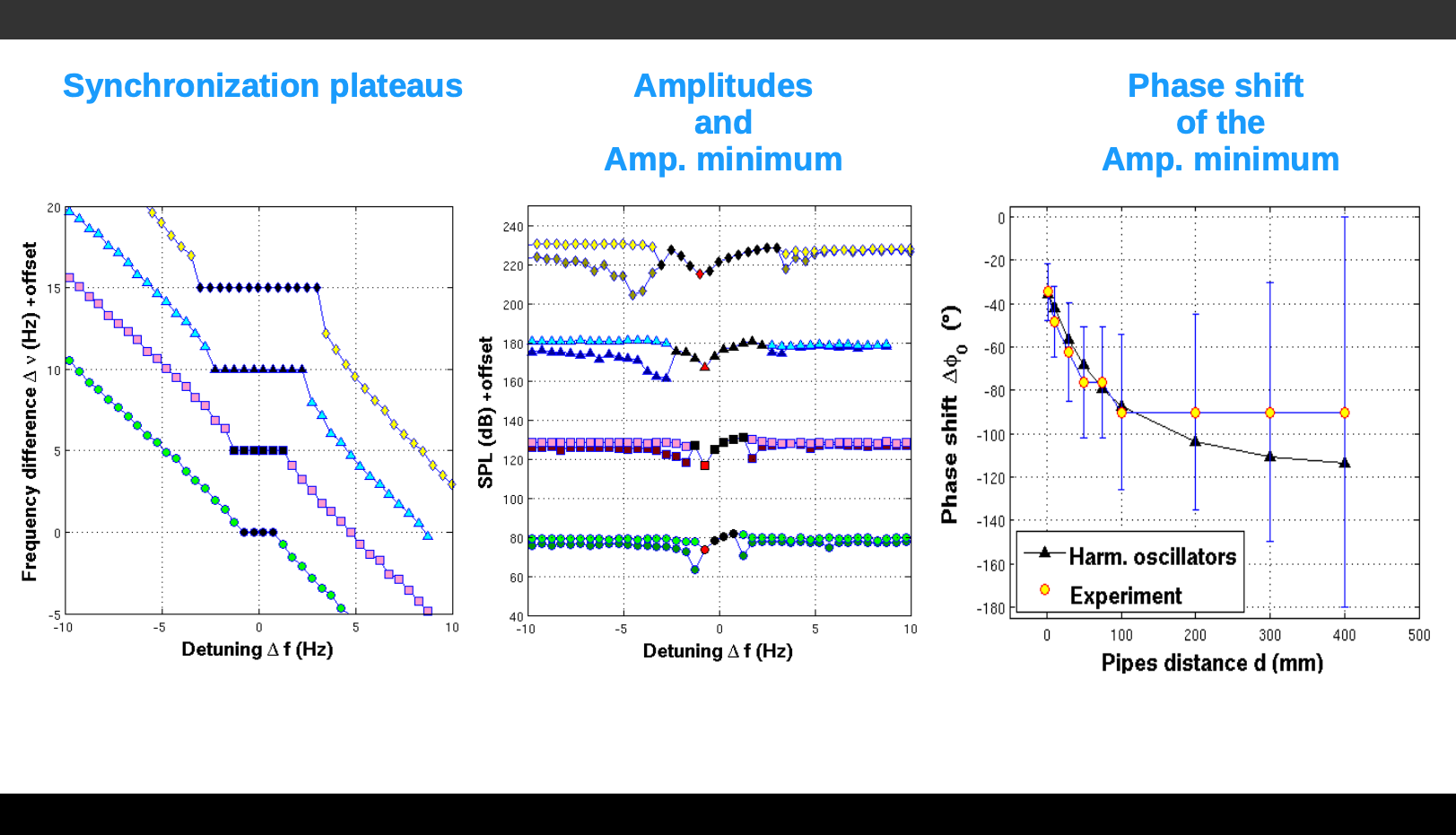
The synchronization plateaus form a structure, called Arnold tongue, which gives informations about the coupling parameters.

With the coupling parameters one can model the coupling between the instuments.
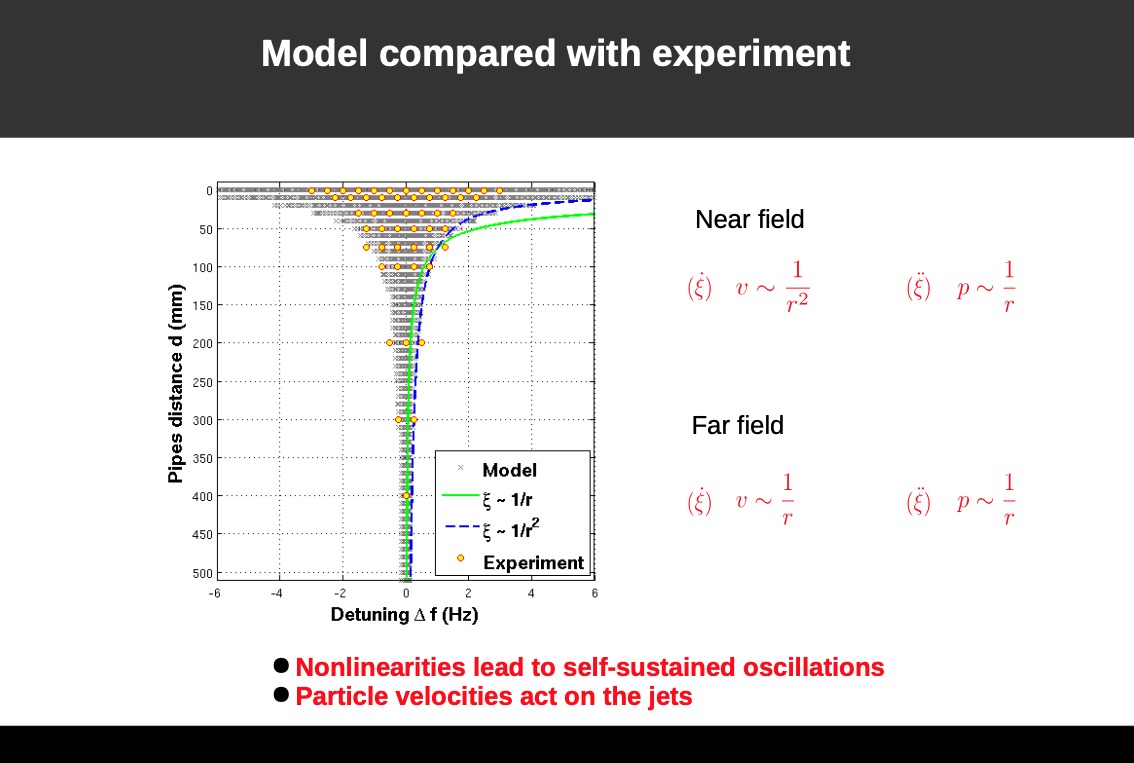
From phase data we reconstruct the oscillator model and the nonlinear coupling function.
